| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- stack 스택
- 바텀업
- 주석
- 피보나치수열
- 디피
- 메모이제이션
- 영어말하기
- 오픽노잼공부방법
- 오픽가격
- 탑다운
- dp
- 이진탐색
- 오픽노잼
- opic
- English
- fibo
- dynamicProgramming
- 안드로이드주석
- 안드로이드
- 이진탐색 #나무 자르기
- 오픽공부법
- 오픽
- topdown
- XML주석
- 영어회화
- 다이나믹프로그래밍
- ㅂ
- XML
- 오픽점수잘받는방법
RUBY
[R] 2. 데이터의 관리와 이해 | 벡터/팩터/배열/행렬/데이터프레임/R을 활용한 머신러닝 본문
-데이터 저장에 사용하는 R의 기본 데이터 구조의 사용방법
-실용적인 내용으로 데이터를 R로 가져오고 R애서 내보내는 데 도움이 되는 함수
-복잡한 데이터를 이해하고 시각화하는 전형적인 방법
*R의 데이터 구조
1.vector
2.factor
3.array and matrix
4. data frame
1. Vector
: element(항목)이라고 하는 값의 순서 집합(ordered set)을 저장한다.
-백터 항목은 개수 제한이 없으며 모두 같은 타입이어야 한다. =숫자와 텍스트 동시에 가질 수 없음
-벡터 v의 타입 판단 typeof(v)
-벡터 타입->①integer ②double ③character ④logical(True false) ⑤NULL(값이 존재하지 않음) ⑥NA(결측치)
-c():작은벡터 결합함수로 만들 수 있음
- <- : 벡터의 이름 화살표 연산자로 부여,assignment(대입)하는 방식
2. Factor(팩터)
-명목(nominal): 특징이 범주 값을 갖는 특성
-팩터(factor): 오직 범주 변수나 순위 변수만을 나타내기 위해 사용되는 특별한 종류의 벡터
-장점) 범주 레이블 한 번만 저장
-머신 러닝은 명목 데이터와 수치 데이터를 다르게 취급
-factor(): 문자 벡터에서 팩터를 생성하는 것
-levels: factor가 가질 수 있는 가능한 범주의 집합 구성
-팩터 데이터 구조는 명목 변수의 범주 순서 정보를 가질 수 있어서 순위데이터를 저장
3.리스트
: 항목의 순서집합을 저장
-벡터: 모든 항목이 같은 타입, 리스트: 수집될 항목이 다른 타입이여도됨.
-리스트 구조: 환자의 모든 데이터를 하나의 객체로 묶어 반복적으로 사용할 수 있음.
-c() 함수로 벡터를 생성하는 것처럼 list()함수로 리스트를 생성할 수 있음
-리스트를 구성할 때 열의 각 구성 요소에는 이름이 주어진다.
-기본 데이터 타입을 갖는 하나의 리스트 항목을 반환하려면 리스트의 구성 요소를 선택할 때 이중괄호 [[]]를 사용
-리스트 구성 요소에 접근할 때 $와 리스트 구성 요소 이름을 리스트 이름에 붙여서 직접 접근한다.
subject1$temperature
-이름 벡터를 명시해 리스트의 여러 항목을 얻을 수 있다
Subject1[c(“temperature”,”flu_status”)]
4 .데이터 프레임(data frame)
: 데이터의 행과 열을 가지고 있기 때문에 스프레드 시트나 데이터베이스와 유사
-정확한 동일한 개수의 값을 갖는 벡터나 팩터의 리스트
-데이터 프레임은 벡터 타입 객체의 리스트
-data.frame() : 벡터를 하나의 데이터 프레임으로 합쳐줌
-stringAsFactors: R은 모든 문자 벡터를 팩터로 자동적용 하기 때문에 false를 주면 이를 방지한다.
-2차원->추출 원하는 행/열을 모두 명시해야 한다, 행렬형식
-데이터 프레임의 열-> 특징(feature),속성(attribute) , 행-> 예시(example)

-리스트와 비슷하게 데이터 프레임에서 여러 열 추출 시
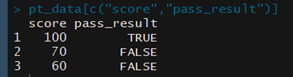
-전체 추출 시

-첫번째 행의 모든 열 추출 시


5.행렬과 배열
-행렬: 데이터의 행과 열을 갖는 2차원 표를 나타내는 데이터 구조
-matrix(): 행의 개수(nrow), 열의 개수(ncol)를 명시하는 파라미터와 데이터 벡터 제공
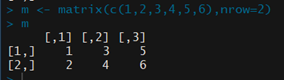
*데이터 구조 저장,로드,제거
-save() : 데이터 구조를 파일로 저장해 다시 로드하거나 다른 시스템에 전송할 수 있게 하는 것, file파라미터로 지정된 위치에 한 개이상의 데이터 구조를 저장한다, .RDdata확장자 가진다.
save(x,y,z, file=”mydata.RData”)
-load(): .RData 파일에 저장된 데이터 구조를 재생성
load(“mydata.RData”)
-ls(): 목록화 함수, 현재 메모리에 있는 모든 데이터 반환
-rm(): 데이터 구조가 클 경우 메모리 해제 시, 제거해야 할 객체의 이름 문자 벡터 제공 시
*csv파일에서 데이터 가져오기와 저장하기
-각 라인의 특징값, 구분자(delimiter) 기호에 의해 분리
-header 라인 첫번째 라인에는 데이터의 열 이름 나열
-csv: 가장 일반적인 표 형식의 텍스트 파일
-read.csv(): csv파일이 있을 때 파일을 R로 로드 , read.table()함수의 특별한 경우
pt_data<-read.csv(“pt_data.csv”,stringAsFactors=FALSE)
-read.table(): 탭 구분값과 같이 다양한 구분자 형식을 포함하는 여러 형태의 표 데이터
-write.csv(): 데이터 프레임을 csv파일에 저장
write.csv(pt_data, file=“pt_data.csv”,row.names=FALSE)

*데이터 구조 탐색
-data dictionary: dataset의 특징을 설명
-str(): data frame, vector, list와 같은 R데이터 구조를 보여준다.

-chr레이블: 특징이 character타입이라는 것을 말해줌
*수치변수탐색
-summary():일반적인 요약 통계를 보여줌 ,여섯 개의 요약통계 조사 위한 간단하면서 강력한 툴
중심측정 퍼짐측정 두가지로 나뉨

-중심경향의 측정(central tendency): 데이터셋의 가운데에 있는 값을 식별하는 데 사용하는 통계부류, 중심 척도는 평균(산술평균, 기하 평균, 조화 평균, 중앙값,최빈값)
-mean(): 숫자 벡터에 대한 평균 계산

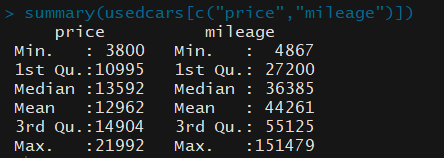
-평균 vs 중앙값: 평균은 이상치에 민감, 소수의 극값으로 더 높게, 낮게 이동할 가능성이 있음,평균은 중앙값보다 극값에 민감,하기 때문에 더 높은 쪽으로 당겨지지만, 중앙값은 동일한 위치에 있음
*퍼짐측정: 사분위수와 다섯 숫자 요약
-중심척도(평균,중앙값)은 측정치에 다양성이 있는지 거의 말해주지 않음
-five-number summary
①최솟값
②1사분위 Q1
③중앙값 Q2
④4사분위 Q3
⑤MAX
-min(), max(): 데이터 벡터에 대해 최솟값과 최댓값을 계산
-range: 최솟값과 최댓값의 사이의 폭
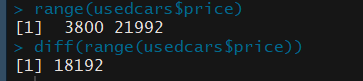
-range(): 최솟값과 최댓값을 같이 반환
-range() 와 diff()를 이용한 데이터 범위
:diff(range(usedcars$price))
-사분위수: 데이터셋을 네 부분으로 나누고 각 부분은 같은 개수의 값, 분위수라는 통계 유형의 특별한 경우
-분위수(quantiles): 통계 유형의 특별한 경우, 데이터를 같은 크기의 수량으로 나누는 숫자
-IQR,Interquartile Range(사분위 수 범위), IQR(): Q1과 Q3의 차이
-quantile() 일련의 값에 대해 분위수를 식별하는 강력한 툴 제공
-cut point 나타내는 probs 파라미터 명시하면 임의의 분위수를 얻을 수 있음

quantile(usedcars$price,probs=c(0.01,0.99)
-seq(): 균등한 간격을 갖는 값들의 백터를 생성
quantile(usedcars$price, seq(from=0,to=1,by=0.20)
*수치 변수 시각화: 상자그림
-boxplot(상자그림)/box-and-whiskers plot(상자수염그림): 다섯 숫자 요약을 일반적으로 시각화한 것, boxplot은 변수의 중심과 퍼짐을 보여줄 때 변수의 range 와 skew를 이해할 수 있고, 다른 변수와 비교할 수 있는 형식으로 보여줌, 변수에 대한 상자그림을 얻을 때
-main,ylab 파라미터를 명시하면 그림 제목과 y축 레이블을 추가 할 수 있음
> boxplot(usedcars$price,main="Boxplot of Used Car Prices")

> boxplot(usedcars$mileage,main="Boxplot of Used Car Mileage",ylab="Odometer (mi.)")

-box-and-whiskers plot : 다섯가지 요약 값을 가로선과 점으로 보여준다 가운데 있는 상자를 구성하는 가로선은 맨 아래에서 맨 위로 그림을 읽을 때 Q1,Q2(중앙값),Q3 를 나타낸다.
*수치 변수 시각화: 히스토그램
-히스토그램: 수치 변수의 퍼짐을 그래프로 그리는 방법
-미리 개수가 정해진 부분 또는 빈으로 변수 값을 나눈다는 점에서 상자그림과 비슷하고 빈(bin)은 값에 대한 컨테이너 역할
-box plot은 데이터의 네 부분이 각각 같은 개수의 값을 포함, 필요한 만큼 bin을 넓히거나 줄일 수 있는 반면 히스토그램은 동일한 폭의 빈을 개수의 제한 없이 사용, 빈에 포함된 개수가 다름
-값의 개수 또는 빈도를 나타내는 높이를 갖는 일련의 막대로 구성, 값이 소속되어 있는 균등한 폭의 bin들이 전체 값을 분할
-skew(왜도): 데이터가 쏠려있는 것, right skew :오른쪽으로 꼬리가긴, no skew: 좌우 대칭, left skew: 왼쪽으로 꼬리가 긴
hist(usedcars$price,main="Histogram of Used Car Prices", xlab= "Price($)")



*수치 데이터의 이해: 균등 분포와 정규 분포
-변수의 분포(distribution): 값이 다양한 범위 내에 속할 확률
-균등(uniform): 모든 값이 동일하게 발생
-normal distribution: 가운데 막대의 양쪽에서 점점 멀어지면서 값의 발생 가능성이 낮아지는 종모양의 데이터 분포
*퍼짐 측정: 분산과 표준편차
-분포는 소수의 파라미터로 다수의 값을 특성화
-정규분포는 중심과 퍼짐이라는 두 파라미터 만으로 정의 , 중심은 평균으로 정의
-퍼짐은 standard deviation 통계로 측정
-표준편차를 계산하려면 분산(variance) 구해야한다.
-분산: 각 값과 평균의 차에 대한 제곱의 평균으로 정의
-var() , sd(): r에서 분산과 표준편차를 얻기 위해서 사용, 분산을 해석할 때 큰 숫자는 데이터가 평균 주변에 좀 더 넓게 퍼져 있음, 표준 편차는 대략 값이 평균과 어떻게 다른지 나타냄

*범주 변수 탐색
-범주형 데이터: 요약 통계가 아닌 표를 이용한 관찰
-일원배치표: 단일 범주 변수를 나타내는 표
-table(): 단방향 표 생성 시, 명목 변수의 범주와 범주에 속하는 값의 개수 나열
-prop.table() : 직접 표 비율 계산


*중앙화 경향 측정: 최빈값
-최빈값: 가장 빈번히 발생하는 값
-평균과 중앙값이 명목변수에는 정의 되지 않기 때문에 최빈값은 범주 데이터에 자주 사용
-단봉(unimodal) :최빈값을 하나 갖는 변수
-양봉(bimodal): 최빈값이 두개인 변수
-다봉(multimodal): 최빈값이 여러 개인 데이터
-데이터가 다봉인지 아닌지를 조사하기위해 최빈값을 고려해보기
*변수 간의 관계 탐색
-이변량 관계: 두 변수간의 관계 고려
-다변량 관계: 두개 이상의 변수 관계
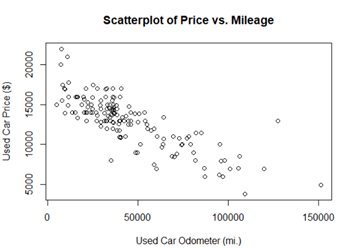
*관계 시각화: 산포도
-산포도: 이변량 관계를 시각화하는 다이어그램, 수평적 x좌표를 제공하는 특징 값과 수직 y좌표를 제공하는 특징 값을 이용해 좌표 평면 상에 점들을 그려 놓은 2차원 그림
-plot(): 다이어그램 레이블하기 위함, main xlab,ylab이용
-negative association(음의 관계): 점들의 패턴이 아래로 기울어진 선
-positive association(양의 관계): 위쪽으로 기울어진 선
-correlation: 두 변수간에 선형 관계의 강도
*관계 관찰 : 이원교차표
-이원교차표: 두 명목 변수간의 관계를 관찰하기 위함
-교차표는 하나의 변수 값이 다른 변수 값에 의해 어떻게 변하는지 관찰할 수 있는 산포도와 비슷
-형식은 표로, 행은 한 변수의 level로 이뤄지고 열은 다른 변수의 레벨
-표의 각 셀에 있는 수치는 특정 행과 열의 조합에 해당하는 값의 개수
-%in%연산자: 연산자의 왼쪽 벡터 값이 오른쪽 벡터에 존재하는지 여부에 따라 TRUE FALSE를 반환한다. ->중고차 색이 black, gray,silver,white집합에 있는가?

-CrossTable(): 하나의 표로 행과 열, 주변 백분율을 표현하므로 데이터를 직접 결합하는 번거로움을 덜어준다.

-카이제곱값: 두변수사이의 독립에 대한 피어슨 카이제곱 검정으로 셀의 기여도 나타냄
-표의 셀 개수가 차이가 우연일 가능성 측정, 확률이 낮으면 두 변수가 연관되어 있는 강한 증거 제공
<참고문헌>
브레트 란츠, 윤성진 옮김, 『R을 활
용한 머신러닝』, 에이콘출판주식회사(2017), p31-p63.
'STUDY > R을 활용한 머신러닝' 카테고리의 다른 글
| [R]3. 게으른 학습: 최근접 이웃 분류/k-NN알고리즘 (0) | 2020.08.22 |
|---|---|
| [R] 1. 머신 러닝 소개_머신 러닝 기원/머신 러닝 사례/머신 러닝 윤리/기계학습 방법/R을 활용한 머신 러닝 (0) | 2020.08.19 |
| [R]5. 분할정복: 의사결정 트리와 규칙 기반의 분류 (0) | 2020.08.17 |
| [R]4.확률적 학습: 나이브 베이즈 분류 (0) | 2020.08.13 |



